[TOC]

概述

文章参考：https://blog.csdn.net/wbf1013/article/details/122811230

弧度

在数学中，弧度是角的度量单位。它是由国际单位制导出的单位，单位缩写是rad。

定义：弧长等于半径的弧，其所对的圆心角为1弧度。(即两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时，两条射线的夹角的弧度为1)。

很简单的思考：如果弧长等于半径，拉直的话，就是会形成一个等边三角形，度数是60度。 但是因为是弧形的，对应的角度肯定不到60度。

角度

角度是用以量度角的单位，符号为“ ∘ \circ ∘”。一周角分为360等份，每份定义为1度（ $$1^\circ$$）。
弧度的几何意义是以逆时针为正，以顺时针为负，以 1 1 1 为半径的扇形的弧长是圆心角弧度的绝对值。从而平角的弧度是 π \pi π， 可以给出常用的弧度与角度的关系如下：

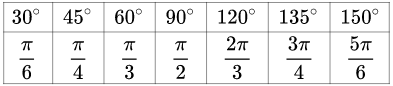
在这里插入图片描述

角度转换

360度=2π弧度(公式一)

1.角度换弧度

根据公式一，可得：1度=（2π弧度）/360=π/180(弧度)

所以：1°=π/180（rad）

2.弧度换角度

根据公式一，可得：1弧度=（360度）/2π=180/π(度)

所以：1rad=180/π（°）= 57.32°

img

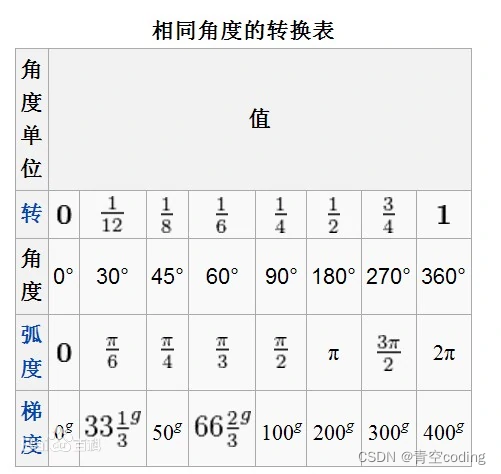
三角函数

1. sin :

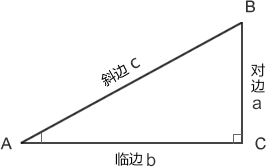
正弦值：对边/斜边

sin A = a/c

img

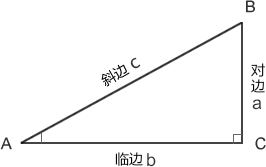
求 30°sin值 ，由于 sin() 函数的参数是弧度，所以在给函数传递参数前，需要先将 30° 转换为弧度值。

1
2
3
4
5
double param, result;
   param = 30.0;
   result = sin (param*PI/180);
   printf ("The sine of %f degrees is %f.\n", param, result );
   return 0;

2. cos

余弦值：cos A = b / c

img

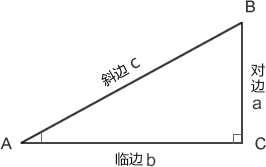
3. tan

正切值：tan A = a/b

img

3. acos、atan、asin同理

反余弦函数 acos() 和余弦函数 cos() 的功能恰好相反：cos() 是已知一个角的弧度值 x，求该角的余弦值 y；而 acos() 是已知一个角的余弦值 y，求该角的弧度值 x。

求0.5的反余弦值

1
2
3
4
5
double param, result;
   param = 0.5;
   result = acos (param) * 180.0 / PI;  //将弧度转换为度
   printf ("The arc cosine of %f is %f degrees.\n", param, result);
   return 0;

5. atan2（反正切值）

反正切函数 atan2() 和正切函数 tan() 的功能正好相反，tan() 是已知一个角的弧度制，求该角的正切值，而atan2是已经知道角的正切值(也就是y/x)，求该角的弧度制。

当 (x, y) 在象限中时：
p

  • 当 (x, y) 在第一象限，0 < θ < π/2
  • 当 (x, y) 在第二象限，π/2 < θ ≤ π
  • 当 (x, y) 在第三象限，-π < θ < -π/2
  • 当 (x, y) 在第四象限，-π/2 < θ < 0